民族

汉

政治面貌

无党派

职称/职务

教授

毕业学校

兰州大学

学位

理学博士

专业

应用数学

研究方向

   非线性偏微分方程

通信地址

yl7703永利官网

邮编

264005

联系电话

05356902406

E-mail

wang_feizhi@126.com

个 人 履 历（从大学填起）

时　间

单位

经　历

1992.09—2002.06

兰州大学

获理学博士学位

2002.07—2004.06

苏州大学

博士后

2004.07—至今

yl7703永利官网

教师

教 学   成 果

科 研   奖 励

              1.  2010年山东省科学技术奖   自然科学 三等奖 (名称：非线性椭圆型微分方程和系统的研究；位次：5/5)

              2.  2012年山东高等学校优秀科研成果   自然科学 一等奖.(名称：非线性椭圆型微分方程的研究；位次：2/2)

              3.  2012年yl7703永利官网科学技术进步   一等奖 (名称：非线性椭圆型微分方程和系统解的定性和定量研究；位次：2/2.)

              4.  2009年山东高等学校优秀科研成果   自然科学 三等奖.(名称：非线性椭圆型微分方程的定性和定量研究；位次：2/3)

              5.     2009年yl7703永利官网优秀科研成果 二等奖 (名称：奇异半正和奇异扰动非线性问题及其应用；位次：2/2.).

科 研   项 目

主持和参与项目：

              1.   山东省自然科学基金 （ZR2011AL009）(名称：非线性Klein-Gordon-Maxwell方程组解的存在性和多解性，时间：2011.12-2014.12；主持)

              2.   国家自然科学基金(10671169) （名称：解在边界blow-up的非线性椭圆性问题；时间：2007.1-2009.12；第三位）

              3.   山东省自然科学基金 （2009ZRB01795）(名称：半线性椭圆型方程爆炸解的二次展式；时间：2009.1-2011.12；第二位)

科 研 论 文

1.    Multiple solutions for   some nonlinear Schrödinger equations with indefinite linear part,
  Journal of Mathematical Analysis and Applications, Volume 331,   Issue 2, 15 July 2007, Pages 1001-1022

2.      Multiple solutions for   some Schrödinger equations with convex and critical nonlinearities in 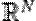, Journal of Mathematical Analysis and Applications, Volume   342, Issue 1, 1 June 2008, Pages 255-276

3.      On an electromagnetic   Schrödinger equation with critical growth , Nonlinear Analysis: Theory, Methods & Applications, Volume   69, Issue 11, 1 December 2008, Pages 4088-4098

4.    Existence results for   singular critical elliptic problems in 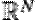, Journal of Mathematical Analysis and Applications, Volume   339, Issue 2, 15 March 2008, Pages 863-875

5.      Solitary waves for the   Klein–Gordon–Maxwell system with critical exponent, Nonlinear Analysis: Theory, Methods & Applications, Volume   74, Issue 3, 1 February 2011, Pages 827-835